Question

A set of equations is given below:Equation M: y = 3x + 4 Equation P: y = 3x + 7Which of the following options is true about the solution to the given set of equations? (4 points)No solutionOne solutionTwo solutionsInfinite solutions

Answer 1

A line equation can be written in slope-intercept form, which is:

`y=mx+b`

where m represents the slope and b the y-intercept.

The solution of a linear system is given by the intercept between the line equations. A linear system can have one solution, when the lines cross each other, infinite solutions when they are the same, or none if they are parallel.

To determinate this, we can use the slope and y-intercept. Given two line equations, if their slopes are different the system has one solution, if the slopes are the same and the y-intercepts are the same the system has infinite solutions, and if the slopes are the same and the y-intercept are different the system has no solutions.

In our system, we have:

`\begin{cases}y={3x+4} \\ y={3x+7}\end{cases}\implies\begin{cases}m_1={m_2}=3 \\ b_1={4\\e b_2=7}\end{cases}`

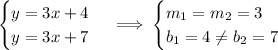
We have the same slope and distinct y-intercepts, therefore, this system has no solution.