Answer:
x = -50/11
y = 17/11
Step-by-step explanation:
We have the following system of equations:
5x - 6y = -32
-3x - 3y = 9
To solve by elimination, we will multiply both sides of the second equation by -2, so:
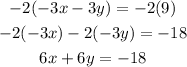
Now, we can add this equation with the first equation, so:
5x - 6x = -32
6x + 6x = -18
11x + 0 = -50
So, solving for x, we get:
11x = - 50
11x/11 = -50/11
x = -50/11
Then, we can replace the value of x by -50/11 on the first equation:
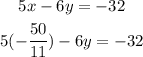
So, solving for y, we get:
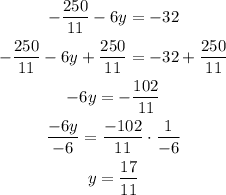
Therefore, the solution of the system is:
x = -50/11
y = 17/11