When we talk about direct variation we mean the following relationship between variables:
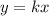
where "k" is a constant. We must determine the value of this constant. To do that, we use the fact that when y = 18, x = 13, we replace that in the relationship:
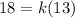
Now we solve for "k", dividing both sides by 13, like this:

solving we get;
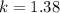
We replace this value in the relationship:
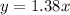
Now we are asked the value of "y", when "x = 63", we replace x = 63 in the relationship, we get:
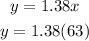
solving we get;

Therefore, y = 87.23 when x = 63