The growth is an exponential growth
(a)
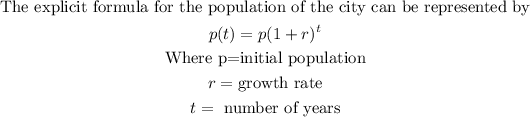
For t years after 2000, at 8.5% growth rate per year , we have
(b) If this trend continues, what will the city's population be in 2016?
from year 2000 to 2016, we have 16 years. Therefore, t=16
put t=16 into p(t) above
we have
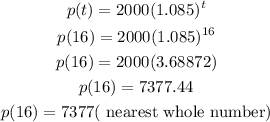
The population of the city in 2016 will be 7377 (to nearest whole number)
When does this model predict city's population to exceed 600 thousand?
This can be interpreted as the year when p(t) is greater than 600,000

This implies that from 70 years from year 2000, the city's population exceed 600 thousand.
In calendar, this will be the year 2070.
Hence, in year 2070 the city's population will exceed 600 thousand.