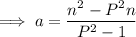Answer:
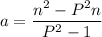
Explanation:
Given equation:
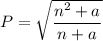
Square both sides of the equation:
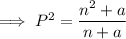
Multiply both sides by (n + a):
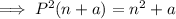
Expand the parentheses:
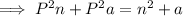
Subtract a from both sides:
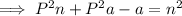
Subtract P²n from both sides:
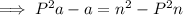
Factor out a on the left side of the equation:

Divide both sides by (P² - 1):