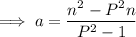Question

Make a the subject of the formula:

P = square root n² + a
____
n+a

Answer 1

`a=(n^2-P^2n)/(P^2-1)`

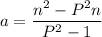
Explanation:

Given equation:

`P=\sqrt{(n^2+a)/(n+a)}`

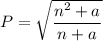
Square both sides of the equation:

`\implies P^2=(n^2+a)/(n+a)`

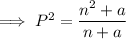
Multiply both sides by (n + a):

`\implies P^2(n+a)=n^2+a`

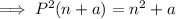
Expand the parentheses:

`\implies P^2n+P^2a=n^2+a`

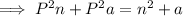
Subtract a from both sides:

`\implies P^2n+P^2a-a=n^2`

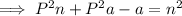
Subtract P²n from both sides:

`\implies P^2a-a=n^2-P^2n`

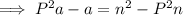
Factor out a on the left side of the equation:

`\implies a(P^2-1)=n^2-P^2n`

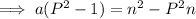
Divide both sides by (P² - 1):

`\implies a=(n^2-P^2n)/(P^2-1)`