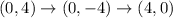We are asked to reflect the vertices of a triangle first across the x-axis and then across the line y = -x. The rule for a reflection across the x-axis is the following:
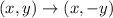
Or
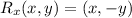
The rule for the reflection across the line y = -x:
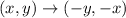
Therefore, applying both transformations we get:
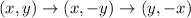
Applying the rule to each point.
For point F(-6,8) we get:
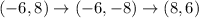
For point G(-3,-1):
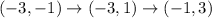
For point H(0,4) we get: