Question

C is the circumcenter of APQR.PC=3x+7, RC=5x-15, & QC=51-Xogx=[? ]

Answer 1

Ok, so

Drawing the situation given:

Now, we want to find the value of x.

First, remember that the circumcenter of a triangle, is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect.

Now, we could apply this definition to find the value of x.

We know that PC = 3x+7 , RC = 5x-15, and QC = 51-x.

We could start by noticing that if C is the circumcenter of the triangle, then:

`PC=QC=RC`

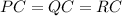
That's because all vertices of a triangle are equidistant from its circumcenter.

So, it is true that:

`\begin{gathered} 3x+7=5x-15=51-x \\ 3x+7=51-x \\ 4x=44 \\ x=11 \end{gathered}`

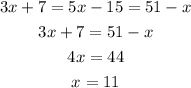
Notice that if we equal other equations, the result will be the same one.

`\begin{gathered} 3x+7=5x-15 \\ 22=2x \\ x=11 \end{gathered}`

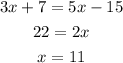
Therefore, x=11.