Question

I need help with this practiceThe subject is complex numbers and vectors*It asks to fill in the four boxes, *enter the roots in order of increasing angle measure

Answer 1

`\begin{gathered} \:\sqrt[4]{4}cis\left(-(\pi )/(24)\right)\: \\ \\ \:\sqrt[4]{4}cis\left((11\pi)/(24)\right)\: \\ \\ \:\sqrt[4]{4}cis\left((23\pi)/(24)\right)\: \\ \\ \:\sqrt[4]{4}cis\left((35\pi)/(24)\right)\: \end{gathered}`

Explanation:

We have the following expression:

`2√(3)-2i`

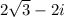
To calculate the 4 roots we must match the equation with x raised to 4, just like this:

`x^4=2√(3)-2i`

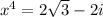
For this case the roots are given as follows:

`\begin{gathered} \:z_k=\sqrt[n]a\right\left(\cos\left((\arctan\left(\alpha\right)+2k\pi)/(n)\right)+i\sin\left((\arctan\left(\alpha\right)+2k\pi)/(n)\right)\right) \\ \\ \text{ In this case:} \\ \\ n=4 \\ \\ |a|=\sqrt{\left(2√(3)\right)^2+\left(-2\right)^2}=√(12+4)=√(16) \\ \\ a=4 \\ \\ \alpha=\left((-2)/(2√(3))\right) \\ \\ \text{ Therefore:} \\ \\ \arctan\left((-2)/(2√(3))\right)=-(\pi)/(6) \end{gathered}`

Taking into account the above, we calculate for each x,

when k = 0,1, 2 3, just like this: