Question

Miguel measured the amount of gas his car used when he drove it for various distances. He recorded his data in the table below.Miles Gallons ofDriven Gas Used200.6735 1.17401.3345 1.50Which is the best conclusion based on the data in the table?O A. The gas mileage that Miguel's car gets decreases as the amount of miles that it has traveled increases.OB. The amount of gas Miguel's car uses is a quadratic function of the amount of miles it travels.OC. The amount of gas Miguel's car uses is a linear function of the amount of miles it travels.D. The gas mileage that Miguel's car gets increasesthe amount of miles that it has traveled increases.

Answer 1

Given data:

When 20 miles were driven, 0.67 gallons of gas was used

when 35 miles were driven, 1.17 gallons of gas was used

when 40 miles were driven, 1.33 gallons of gas was used

when 45 miles were driven, 1.50 gallons of gas was used

Step 1: Find the unit rate of a gallon per mile

`(0.67)/(20)=0.033\text{ gallon/mile}`
`(1.17)/(35)=0.033\text{ gallon/mile}`
`(1.33)/(40)=0.033\text{ gallon/mile}`

`(1.5)/(45)=\text{ 0.033 gallon/mile}`

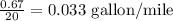
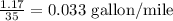
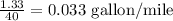
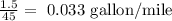
Step 2: Compare the unit rates obtained

We can see that the amount of gas used per mile is constant (0.033gallon per mile),

Hence, The amount of gas Miguel's car uses is a linear function of the amount of miles it travels