Question

A 3,000 kg truck moving at +10m/s hits a 1,000 kg parked car which moved off at +15m/s. What is the velocity of the truck

Answer 1

Given,

The mass of the truck, M=3000 kg

The mass of the car, m=1000 kg

The velocity of the truck before the collision, u=10 m/s

The velocity of the car after the collision, v₁=15 m/s

From the law of conservation of momentum, the total momentum of the car and the truck before the collision is equal to their total momentum after the collision.

Thus,

`Mu=mv_1+Mv_2`

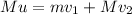
Where v₂ is the velocity of the truck after the collision.

On rearranging the above equation,

`v_2=(Mu-mv_1)/(M)`

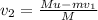
On substituting the known values,

`\begin{gathered} v_2=(3000*10-1000*15)/(3000) \\ =5\text{ m/s} \end{gathered}`

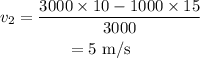
Therefore the velocity of the truck after it hits the car is 5 m/s