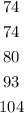Question

Five students stepped onto five scales. Wyn, Chen, Ramon and two Gails. Rather than list all their weights, they summed up their data to state: Range: 30 Mode: 74 Median: 80 Mean: 85 And now we would like you to say how much each of the five might weigh.

Answer 1

3 clear values ​​are the mean and at least two values ​​of 74 since it is the mode

`\begin{gathered} 74 \\ 74 \\ 80 \\ a \\ b \end{gathered}`

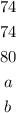
if the range is 30 the difference between 74 and greater number is 30

then

`\begin{gathered} b-74=30 \\ b=104 \end{gathered}`
`\begin{gathered} 74 \\ 74 \\ 80 \\ a \\ 104 \end{gathered}`

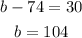
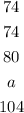
now we apply the mean to find a

we add all numbers and divide between 5 to obtain the mean(85)

`\begin{gathered} (74+74+80+104+a)/(5)=85 \\ \\ (332+a)/(5)=85 \end{gathered}`

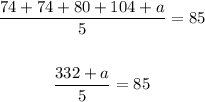
and solve for a

`\begin{gathered} 332+a=85*5 \\ 332+a=425 \\ a=425-332 \\ a=93 \end{gathered}`

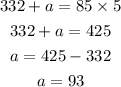
Finall data is

`\begin{gathered} 74 \\ 74 \\ 80 \\ 93 \\ 104 \end{gathered}`