Question

Question for practice class work at homethe question is number #14

Answer 1

Question 14.

Given:

• Frequency, f = 78.0 kHz.

,

• Wavelength, λ = 0.333 m

,

• Speed of sound in air = 344 m/s

Let's find the wave speed and how much faster is the speed than the speed of sound in air.

To find the wave speed, apply the formula:

`\lambda=(v)/(f)`

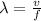
Where:

• v is the wave speed in m/s.

,

• f is the frequency in Hz.

,

• λ is the wavelength in meters (m).

Rewrite the formula for v and solve.

We have:

`\begin{gathered} v=\lambda *f \\ \\ v=0.333*78*10^3 \\ \\ v=25974\text{ m/s} \end{gathered}`

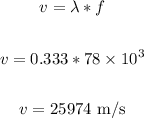
Therefore, the speed of sound in solid is 25974 m/s.

Now, to find how much faster it is, we have:

`\frac{speed\text{ of sound in solid}}{speed\text{ of sound in air}}=\frac{25974\text{ m/s}}{344\text{ m/s}}=75.5`

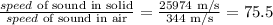
Therefore, it is 75.5 times faster than the speed of sound in air.

ANSWER:

• Speed of sound in solid: , 25974 m/s.

• 75.5, times faster than the speed of sound in air