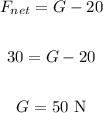In order to calculate the missing forces, we need to know that the net force is the sum of all forces in a direction.
For the first situation, the net force is zero, so the sum of forces in each direction is zero.
In the vertical direction, we have:
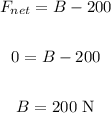
In the horizontal direction:
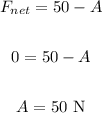
For the second situation, the net force is 900 N up.
In the vertical direction, we have:
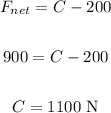
In the horizontal direction, we have no forces.
For the third situation, the net force is 60 N to the left.
In the vertical direction, we have:
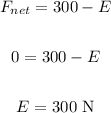
In the horizontal direction, we have:
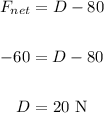
For the fourth situation, the net force is 30 N to the right.
In the vertical direction, we have:
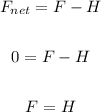
In the horizontal direction, we have: