Part A
Initial population of parrot in the animal sanctuary = 20 parrots
The population is increasing by 5 parrots per year.
let
number of years = x
y = population of parrot
The function can be represented as
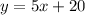
Part B.
Initial population of snake in the sanctuary = 24
Each year 4 more snakes are born
let
number of year = x
y = population of the snake
The function can be represented below
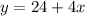
Part C
Number of parrot in 10 years
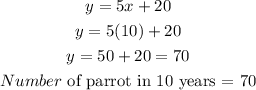
Number of snakes in 10 years
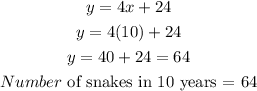
Part D
The number of year where the number of parrot and snakes are the same can be calculated below
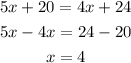
The snakes and the parrot will be equal in population after 4 years time.