Answer: The radius of the circular top is 3.45cm
Step-by-step explanation
• Surface area (SA): 312cm².
,
• Height (h): 11cm.
A can of beans can be approximated to a cylinder figure. Then, the cylinder has a formula for its surface area (SA), which is:
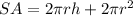
where r represents the radius and h represents the height.
As we have the value for SA and h we can replace them in the formula:
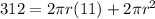
Simplifying the expression by multiplying the parenthesis:

As we have a second-degree polynomial, we can use the General Quadratic Formula to find the solution for r. In order to do so, we have to set the equation to 0 as follows:

where a, b and c are used in the General Quadratic Formula:
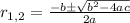
In our case, our equation is:
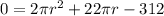
where a = 2π, b = 22π, and c = -312.
Then, replacing these values in the General Quadratic formula we get:
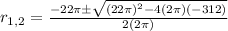
Simplifying the terms inside the square root and the denominator:
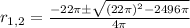
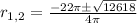
Finally, finding both solutions:

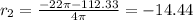
As we cannot have a negative radius, then the correct answer is that the radius measures 3.44cm