Question

y = 1/3x + 2y = -3x^2 – 5x – 4Solve the system by graphing. Can anyone please help with the second on?

Answer 1

For this case we can set up equal the two equations and we got:

`(1)/(3)x+2=-3x^2-5x-4`

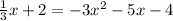
And solving for x w ehave:

`3x^2+(16)/(3)x+6=0`

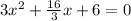
We can multiply both sides of the equation by 3 and we got:

`9x^2+16x+18=0`

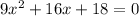
And we can solve this using the quadratic formula and we got:

`x=\frac{-16\pm\sqrt[]{16^2-4(9)(18)}}{2\cdot9}`

Since the discriminant is lower than 0 we can conclude that this system has 0 solutions and we can verify with the graph given by: