Question

Find the possible coordinates of PI’m struggling to do the second part of this question and would like some assistance please

Answer 1

we have the equation of curve C

`y=x^3-11x+1`

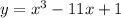
Part a

Find out the gradient, where x=3

To find the gradient, take the derivative of the function with respect to x, then substitute the x-coordinate of the point of interest for the x values in the derivative

so

the first derivative is equal to

`y^(\prime)=3x^2-11`

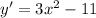
Evaluate the first derivative for x=3

`\begin{gathered} y^(\prime)=3(3^2)-11 \\ y^(\prime)=16 \end{gathered}`

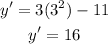
the gradient is equal to 16

Part b

we know that the gradient is equal to 1 at point P

so

equate the first derivative to 1

`\begin{gathered} y^(\prime)=3x^2-11 \\ 3x^2-11=1 \\ 3x^2=12 \\ x^2=4 \\ x=\pm2 \end{gathered}`

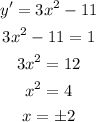
Find out the possible y-coordinate of point P

For x=2

substitute in the given equation of C

`\begin{gathered} y=2^3-11(2)+1 \\ y=8-22+1 \\ y=-13 \end{gathered}`

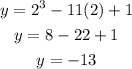
the first possible coordinate of P is (2,-13)

For x=-2

`\begin{gathered} y=-2^3-11(-2)+1 \\ y=-8+22+1 \\ y=15 \end{gathered}`

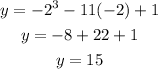
the second possible coordinate of P is (-2,13)