Question

The ideal gas law predicts gas behavior including the relationships between the number of moles, volume, pressure, and temperature.

Answer 1

The volume of the ballon is 4.48L.

Step-by-step explanation:

1st) It is necessary to make sure that all the variables units are in atm, L, mol and K. So, we have to convert 0.00°C to K:

`0.00+273.15=275.15K`

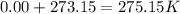
2nd) With the ideal gas formula, we can replace the values of pressure, number of moles and temperature, to calculate the volume of the helium gas in the ballon:

`\begin{gathered} P*V=n*R*T \\ 1.00atm*V=0.200mol*0.082(atm*L)/(mol*K)*273.15K \\ 1.00atm*V=4.48atm*L \\ V=(4.48atm*L)/(1.00atm) \\ V=4.48L \end{gathered}`

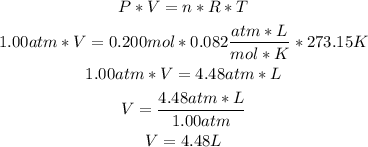
R in the formula is the ideal gas constant, and it is equal to 0.082 atm*L/mol*K.

So, the volume of the ballon is 4.48L.