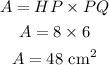Answer
48 cm²
Explanation
First, we need to calculate the height of the parallelogram, segment HP. Applying the Pythagorean theorem to triangle HPQ, we get:
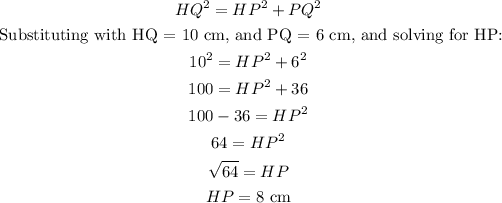
The area of a parallelogram is calculated as follows:
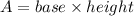
In this case, the height is HP = 8 cm, and the base is PQ = 6 cm. Then the area of parallelogram PQRS is: