Functions:
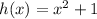
![h^(-1)(x)=\pm\sqrt[]{x-1}](https://img.qammunity.org/2023/formulas/mathematics/college/w2lsg50h6r8xn6a356wqd2swa0ll8i7wbr.png)
The inverse function's graph has to be symmetrical across the y = x line, if we graph this line with the previous graphs:
where the red line is h(x), the blue and green are the possibilities:
![h^(-1)(x)=+\sqrt[]{x-1}](https://img.qammunity.org/2023/formulas/mathematics/college/4a5auooks32acvq0qs73kvw5tynz9bxbmr.png)
...and...
![h^(-1)(x)=-\sqrt[]{x-1}](https://img.qammunity.org/2023/formulas/mathematics/college/4nnhd76z2vxl582t6c2ueuwudunr1lb5xs.png)
...respectively. And the purple line is the line y = x.
As the inverse functions are symmetrical across the y = x line, then we know our functions are inverse.
Answer:
![h^(-1)(x)=\pm\sqrt[]{x-1}](https://img.qammunity.org/2023/formulas/mathematics/college/w2lsg50h6r8xn6a356wqd2swa0ll8i7wbr.png)
• Graph
Reason why it is inverse: the functions are symmetrical across the y = x line.