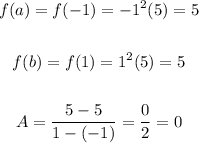Question

Drag each tile to the correct box. Arrange these functions from the greatest to the least value based on the average rate of change in the specified interval. f(x) = x² + 3x interval: (-2, 3] f(x) = 3x - 8 interval: [4, 5] f(x) = x² - 2x interval: (-3,4) f(x) = x².5 interval: [-1.1)

Answer 1

To find the average rate of change, use the formula:

`A=(f(b)-f(a))/(b-a)`

`\begin{gathered} f(x)=x^2+3x \\ \end{gathered}`

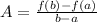
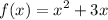
Interval, (a, b) = (-2, 3]

Let's find the average rate of change:

`\begin{gathered} f(a)=f(-2)=-2^2+3(-2)=4\text{ - 6 = -2} \\ \\ f(b)=f(3)=3^2+3(3)=9+9=18 \end{gathered}`

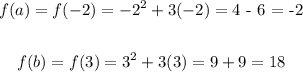
Average rate of change is:

`A=(18-(-2))/(3-(-2))=(18+2)/(3+2)=(20)/(5)=4`

`f(x)=3x\text{ - 8}`

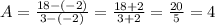
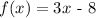
Interval, (a, b) = [4,5]

Let's solve for f(a) and f(b):

`\begin{gathered} f(a)=f(4)=3(4)-8=12-8=4 \\ \\ f(b)=f(5)=3(5)-8=15-8=7 \end{gathered}`

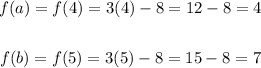
Average rate of change =

`A=(f(b)-f(a))/(b-a)=(7-4)/(5-4)=(3)/(1)=3`

`f\mleft(x\mright)=x^2-2x`

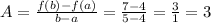
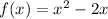
interval, (a,b) = (-3, 4)

Solve for f(a) and f(b)

`\begin{gathered} f(a)=f(-3)=-3^2-2(-3)=9+6=15 \\ \\ f(b)=f(4)=4^2-2(4)=16-8=8 \\ \\ A=(8-15)/(4-(-3))=(8-15)/(4+3)=(-7)/(7)=-1 \end{gathered}`
`f(x)=x^2(5)`

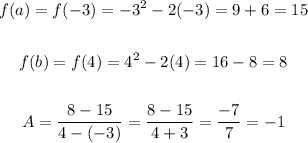
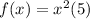
interval, (a,b) =[-1, 1)

`\begin{gathered} f(a)=f(-1)=-1^2(5)=5 \\ \\ f(b)=f(1)=1^2(5)=5 \\ \\ A=(5-5)/(1-(-1))=(0)/(2)=0 \end{gathered}`