Question

In a large school it was found that 70% of students are taken to math class 80% of students are taken in English class and 66% of students are taken both find the probability that a randomly selected student is taking a math class or an English or at class rightly answer as destiny run into 2 decimal places

Answer 1

The answer is:

P{neither Maths nor English) = 0.13

The question tells us that in a school, the proportion of students doing maths is 78%

The proportion of students doing english is 80%

The proportion of students doing both subjects is 66%.

We are then asked to find the probability of students that did neither English nor Maths.

In order to get this value, we must remove the probability of those doing maths and english and also those that are doing both from 1. In other words, we subtract the probability of getting a student in Math or English class from 1.

Let us put this into mathematical expressions:

`\begin{gathered} P(\text{Math)}=(73)/(100) \\ P(\text{English)}=(80)/(100) \\ \\ P(\text{Math and English) = }(66)/(100) \end{gathered}`

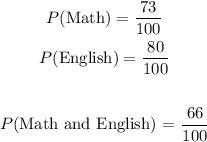
Therefore, we can find the probability of getting a student in either Math or English using the OR probability formula.

The OR probability formula states:

`\begin{gathered} \text{if A and B are independent events,} \\ P(A\text{ OR B) = P(A)+ P(B) - P(A n B)} \\ \text{where,} \\ P(A)=\text{probability that event A occurs} \\ P(B)=\text{probability that event B occurs} \\ P(A\cap B)=\text{probability that both A and B occur} \end{gathered}`

Using P(Math) and P(English) as P(A) and P(B) respectively, we can easily compute the probability that a student is in Math or English class using the above formula.

This is done below:

`\begin{gathered} P(\text{Math or English) = P(Math) +P(English) - P(Math n English)} \\ P(\text{Math)}=(73)/(100) \\ P(\text{English)}=(80)/(100) \\ P(\text{Math}\cap\text{English)}=(66)/(100) \\ \\ \therefore P(\text{Math or English) =}(73)/(100)+(80)/(100)-(66)/(100) \\ \\ P(\text{Math or English) =}(87)/(100)=0.87 \end{gathered}`

Therefore, to find the probability of a student studying neither Maths nor English,

we simply subtract P(Math or English) from 1.

This is done below:

`\begin{gathered} P(\text{neither Maths nor English) = 1 - P(Maths or English)} \\ P(\text{neither Maths nor English)=1 - 0.87} \\ \\ \therefore P(\text{neither Maths nor English)}=0.13 \end{gathered}`

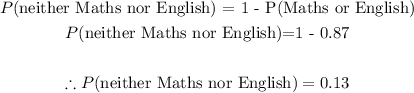
Therefore, the final answer is:

P{neither Maths nor English) = 0.13