Question

Find the number of ground miles from a point directly below the plain to the radar station

Answer 1

The distance from the place and the radar station is 160 miles and the angle of depression is 34º

The distance of the plane to the ground, the horizontal distance between the plane and the radar station, and the direct distance from the plane to the radar station form a right triangle.

The angle of depression is the angle from the horizontal downward an object (radar station) from the point of view of an observer (plane)

You have to determine the horizontal distance between the plane and the radar station, since that side is opposite to the known angle, use the trigonometric ratio that relates the hypotenuse with the opposite side of an angle. That would be the sine

`\sin \theta=\frac{\text{opposite}}{\text{hypothenuse}}`

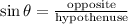
Where

θ is the angle

"opposite" refers to the side that does not interact with the angle

"hypothenuse" is the distance between the plane and the radar station

Replace the expression with the known measures

`\sin 34=(x)/(160)`

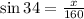
Multiply both sides by 160 to determine the value of x

`\begin{gathered} 160\cdot\sin 34=x \\ x=89.47 \end{gathered}`

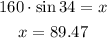
The ground distance between the plane and the radar station is 89.47 miles