Question

The average score on stats midterm was 73 points with standard deviation of 6 points, and your z-score was 2. How many points did you score?

Answer 1

Given:

Mean score, μ = 73

Standard deviation, σ = 6

z-score = 2

Let's find the number of points you scored.

Apply the z-score formula:

`Z=(x-u)/(\sigma)`

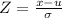
WHere:

x is the actual score

z is the z-score = 2

σ is the standard deviation = 6

μ is the average = 73

Let's rewrite the formula for x, which is the actual score.

Multiply both sides by σ :

`\begin{gathered} Z\sigma=(x-\mu)/(\sigma)\ast\sigma \\ \\ Z\sigma=x-\mu \\ \\ \text{Add }\mu\text{ to both sides:} \\ Z\sigma+\mu=x-\mu+\mu \\ \\ Z\sigma+\mu=x \\ \\ x=Z\sigma+\mu \end{gathered}`

`x=Z\sigma+\mu`

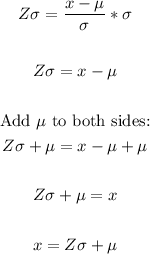
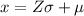
Hence, we have:

`\begin{gathered} x=2(6)+73 \\ \\ x=12+73 \\ \\ x=85 \end{gathered}`

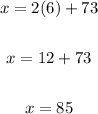
The number of points scored is 85

ANSWER:

85