Question

The parent tangent function is transformed such that its period is halved. Which graph could represent the transformed function?

Answer 1

The tangent function has the following form:

`y=\tan (bx)`

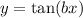
The period of the tangent function is given by:

`P=(\pi)/(b)`

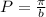
This means that for the parent tangent function:

`y=\tan x`

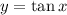
The period is:

`P=\pi`

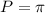
This number represents the distance between two consecutive vertical asymptotes, as shown in the following graph:

If the period is halved this means that the distance between each consecutive asymptote must be half the distance than pi, therefore, it must be:

`P=(\pi)/(2)`

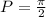
Therefore, the graph must be the following:

and thus we determine the graph of the transformed function-.