At first we should know that :
The product of the slope of the perpendicular lines = -1
Which mean if the slope of one of them is m and the slope of the other is m'
So,
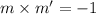
Given : the slope of one line is = m = -5
So, the slope of the perpendicular line will be m'
So,
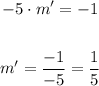
So, the answer is : the slope of the other line = 1/5