Question

Me and Mrs. Taylor hope to send their daughter to college in fourteen years. How much money should they invest now at an interest rate of 9.5% per year, compounded continuously, in order to be able to contribute 8000 dollars towards her education. Do not round any intermediate computation, and round your answer to the nearest cent

Answer 1

They'll have to invest $2,115.82

Explanation:

Remember that the contiuous compounding interest formula is:

`A=Pe^(rt)`

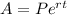
Where:

• A, is the final amount

,

• P, is the initial amount

,

• r, is the rate of interest, as a decimal

,

• t, is the times the interest is compounded

Using this formula and the information given, we'll have that:

`8000=Pe^{((9.5)/(100))(14)}`

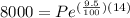
Solving for P,

`\begin{gathered} 8000=Pe^{((9.5)/(100))(14)}\rightarrow\frac{8000}{e^{((9.5)/(100))(14)}}=P \\ \\ \Rightarrow P=2115.82 \end{gathered}`

Therefore, we can conlcude that they'll have to invest $2,115.82