A parabola can have two vertex forms, one for a horizontal parabola and another for a vertical parabola.
The following equation is the vertex form for a horizontal parabola:
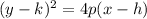
Notice that it fits the given equation, so we know that our parabola is a horizontal one.
In this form, "k" and "h" are the coordinates of the vertex:
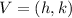
Comparing to the given formula, we can see that:
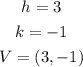
Thus, the first blanck is (3,-1).
Another characterist point of the parabola is its focus, which has the coordinates:

The parabola always opens from the vertex to the focus, so if "p" is positive, the horizontal parabola opens right, and if "p" is negative, the horizontal parabola opens left.
In the given case, we have:
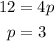
Which means "p" is positive, thus the parabola opens right, so the second blank is right.
Since the Vertex is in (h,k) and the focus in (h+p,k), "p" is also a measure of how many units the focus is from the vertex. Since p = 3, the thrid blank is 3.
The directrix is similar to the focus, but it is a line that passes through a point to the opposit side as of the vertex.
The x value that the directrix passes through is x = h-p, thus "p" is also a measure of how many units the directrix is from the vertex and "2p" is how many units the directrix is from the focus, which is 2*3 = 6 in this case. Thus, the answer in the fourth blank is 6.
As said above, the focus is in the point:
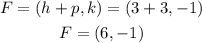
Thus, the fifth blank is (6, -1).
The directrix is a vertical line aat x = h - p, thus it can be written as:

Thus, the sixth blank is x = 0.
Answers:
1: (3,-1)
2: right
3: 3
4: 6
5: (6,-1)
6: x = 0