Question

I’ve had to re do this several times and it’s just not clicking

Answer 1

Since each birth is independent from each other we can use the binomial distribution:

`P\left(X=k\right)=\binom{n}{k}p^k\left(1-p\right)^(n-k)`

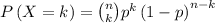
In this case we have 6 births wich mean that n=6, the probability of success is 0.5. With this in mind let's calculate the probabilities we need.

a)

In this case we have:

Therefore, the probability the had at least 3 girls is 0.6563

b)

In this case we have:

`\begin{gathered} P\left(X\leq4\right)=1-P\lparen X>4) \\ =1-P\lparen X=5)-P\left(X=6\right) \\ =1-\binom{6}{5}\left(0.5\right)^5\left(1-0.5\right)^(6-5)-\binom{6}{6}\left(0.5\right)^6\left(1-0.5\right)^(6-6) \\ =0.8906 \end{gathered}`

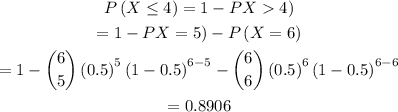
Therefore, the probability the had at most 4 girls is 0.8906