Question

Use the slope-intercept form to graph the equation y=2/9x+3

Answer 1

we are given the following equation of a line

`y=(2)/(9)x+3`

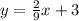
This is written in the slope-intercept form, which means it follows the general form:

`y=mx+b`

Where "m" is the slope and "b" is the intercept. We are asked to find the graph, to do that, we can begin by using the intercept since that is the point where the line touches the y-axis, this means that it represents the point (0,b), in our case, this is: (0,3).

Now we need to find a second point, we can use the point where the line touches the x-axis, that is, the point where y = 0, so we set y = 0 in the equation for the line and solve for "x", like this:

`\begin{gathered} y=(2)/(9)x+3 \\ 0=(2)/(9)x+3 \end{gathered}`

subtracting 3 on both sides

`-3=(2)/(9)x`

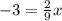
multipliying by 9 on both sides

`-3(9)=2x`

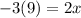
Dividing by 2 on both sides

`\begin{gathered} (-3(9))/(2)=x \\ -(27)/(2)=x \end{gathered}`

therefore, the second point is (-27/2,0). Now we plot both points and join them with a line, like this:

Any two points can be use to plot a line, so one could also use a different value for "x", evaluate that value in the equation for the line and get a value for "y". That point, together with the intercept can be use to plot the line.

We could use for example x = -5, if we replace that value in the equation we get.

`y=(2)/(9)(-5)+3=(17)/(9)`

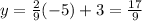
we get the point (-5,17/9), and the plot would look like this: