We will need to translate this to equations, first.
Let x be the fraction of the filed one man cuts in 1 hour.
Let y be the fraction of the filed one boy cuts in 1 hour.
Now, if we have 2 men, they will cut 2x of the filed in 1 hour, and 6x of the field in 3 hours.
And if we have 6 boys, they will cut 6y of the filed in 1 hours, and 18y of the field in 3 hours.
If 2 men and 6 boys cut the whole field in 3 hours, the sum of these quantities have to be 1 field, thus, we have the equation:
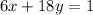
If the men work 3/2 times of the boys, this means that the cut 3/2 more than the boys in 1 hour.
That is, x is 3/2 times y:

With this, we can substitute x into the first equation:
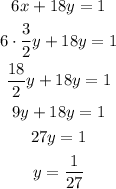
And now, we can use this into the second equation to find out x:
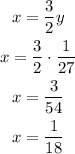
Thus, 1 man cuts 1/18 of the field in 1 hour. In two hours, he cuts twice as much, so he cuts 2/18 which is the same as 1/9.
If we need 1 man to cut 1/9 of the field in 2 hours, we will need 9 men to cut the whole field in 2 hours.
Thus, 9 men are required to cut the field in 2 hours.