Part 1:
The principal is given $5000. The rate of interest is 4%. The interest is compounded monthly.
The formula of the amount after t years at a rate of r is given below:

The amount after 10 years on the principal $5000, at a rate of 0.04 is calculated below:

The amount in the bank after 10 years is $7453.866.
Part 2:
The formula of the amount after t years when the interest is compounding continuously is given below:
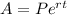
The amount after 2 years in the bank is calculated below:
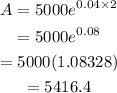
The amount after 2 years in the bank is $5416.4.