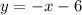The slope between two(2) points;
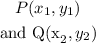
is given as:

From the question, the given points are:
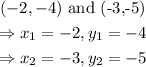
Thus, the slope, m, is:

The equation of a line with two(2) given points is given as:
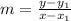
Thus,
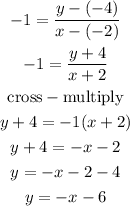
Hence, the slope-intercept form of the equation of the line through the given points is: