You need to remember the following Transformation rules for functions:
1. If
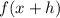
The function is shifted "h" units to the left.
2. If
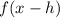
The function is shifted "h" units to the right.
3. If
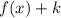
The function is shifted "k" units up.
4. If
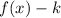
The function is shifted "k" units down.
In this case you have the following Exponential parent function:
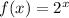
You know that it is shifted 4 units to the right and then 6 units up, then you can identify that the transformations are:
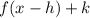
Where
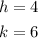
Then, the equation is:
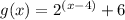
The answer is: Option C.