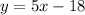The slope-intercept form of a line is expressed as follows;

Where;
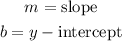
To begin, we shall calculate the slope as shown below;

Using the two points given, we have;
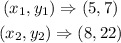
Therefore;
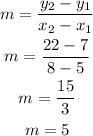
To calculate the y-intercept, we shall insert the value of m into the equation, y = mx + b. We shall use the first point which is (5, 7).
Note that if we use the second point (that is 8, 22) the value of the y-intercept would be the same.
Hence we have;
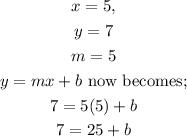
Subtract 25 from both sides;
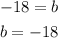
Now that we have the values of m and b, (the slope and the y-intercept), the equation becomes;
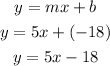
ANSWER:
The correct answer is option (b);