Since the line BC is tangent to the circle we know that the angle CBA is a right angle, hence the triangle is a right one and we can apply the pythagorean theorem.
Now, we know that:

since the radius is 5. Furthermore we also know that:
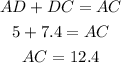
Now, in thie case the pythagoean therorem is:
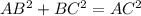
Plugging the values we know and solving for BC we have:
![\begin{gathered} 5^2+BC^2=12.4^2 \\ BC^2=12.4^2-5^2 \\ BC=\sqrt[]{12.4^2-5^2} \\ BC=11.35 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/urfrk62wfol8g72foysjbc9uxa6qd722h3.png)
Therefore BC is 11.35.