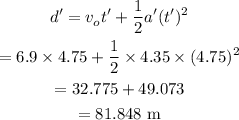Question

A body moves along one dimension with a constant acceleration of 4.35 m/s2 over a time interval. At the end of this interval it has reached a velocity of 13.8 m/s.(a)If its original velocity is 6.90 m/s, what is its displacement (in m) during the time interval? m (b)What is the distance it travels (in m) during this interval? m(c) A second body moves in one dimension, also with a constant acceleration of 4.35 m/s2 , but over some different time interval. Like the first body, its velocity at the end of the interval is 13.8 m/s, but its initial velocity is −6.90 m/s. What is the displacement (in m) of the second body over this interval? m (d) What is the total distance traveled (in m) by the second body in part (c), during the interval in part (c)?

Answer 1

Given that the acceleration of the object is

`a=4.35m/s^2`

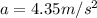
The final velocity is

`v_f=13.8\text{ m/s}`

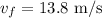
The initial velocity is

`v_o=6.9\text{ m/s}`

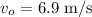
We have to find displacement and distance.

Let the displacement be denoted by S and the distance by d.

First, we need to calculate time in order to find distance and displacement.

The time taken will be

`\begin{gathered} t=((v_f-v_o))/(a) \\ =(13.8-6.9)/(4.35) \\ =1.59\text{ s} \end{gathered}`

(a) The displacement will be

`\begin{gathered} S=v_ot+(1)/(2)at^2 \\ =6.9*1.59+(1)/(2)*4.35*(1.59)^2 \\ =10.971+5.498 \\ =16.469\text{ m} \end{gathered}`

(b) The initial speed will be equal to the initial velocity.

Thus, the distance will be 16.469 m.

(c) The initial velocity of the second object is

`v^(\prime)_o=\text{ -6.9 m/s}`

The final velocity of the second object is

`v^(\prime)_f=13.8\text{ m/s}`

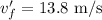
The acceleration of the second object is

`a^(\prime)=\text{ 4.35 m/s}`

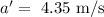
The time taken will be

`\begin{gathered} t^(\prime)=((v_f-v_o))/(a) \\ =\frac{13.8-(-6.9)_{}}{4.35} \\ =4.75\text{ s} \end{gathered}`

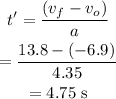
We have to find the displacement of the second object.

Let the displacement of the second object be denoted by S'.

The displacement of the second object will be

`\begin{gathered} S^(\prime)=v^(\prime)_ot^(\prime)+(1)/(2)a^(\prime)(t^(\prime))^2 \\ =-6.9*4.75+(1)/(2)*4.35*(4.75)^2 \\ =-32.775+49.073 \\ =16.298\text{ m} \end{gathered}`

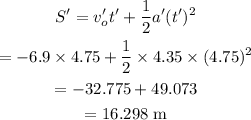
(d) The initial speed of the object will be

`v^(\doubleprime)_o=6.9\text{ m/s}`

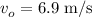
We have to find the distance.

Let the distance be denoted by d'.

The distance of the second object will be

`\begin{gathered} d^(\prime)=v^(\doubleprime)_ot^(\prime)+(1)/(2)a^(\prime)(t^(\prime))^2 \\ =6.9*4.75+(1)/(2)*4.35*(4.75)^2_{} \\ =32.775+49.073 \\ =81.848\text{ m} \end{gathered}`