Question

If Angle LMP = (5x - 19)' and Angle LNP = (2r + 11), find mPL

Answer 1

`\text{mPL}=62\degree`

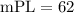
Step-by-step explanation

We want to find the measure of the angle of the arc PL.

To do this, we first have to find the value of x.

We have that:

`\begin{gathered} <\text{LMP}=(5x-19)\degree \\ <\text{LNP}=(2x+11)\degree \end{gathered}`

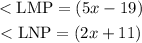
According to circle theorem, the angles subtended at the circumference by the same arc are equal. This means that:

`\begin{gathered} <\text{LMP}=<\text{LNP} \\ \Rightarrow(5x-19)\degree=(2x+11)\degree \end{gathered}`

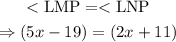
Collect like terms and simplify:

`\begin{gathered} 5x-19=2x+11 \\ 5x-2x=11+19 \\ 3x=30 \end{gathered}`

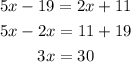
Divide both sides by 3:

`\begin{gathered} (3x)/(3)=(30)/(3) \\ x=10 \end{gathered}`

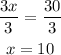
According to circle theorems, we have that the angle of an arc is equal to twice the angle subtended at the circumference by that arc.

This means that:

`\begin{gathered} mPL=2(5x-19) \\ \Rightarrow\text{mPL}=10x-38 \\ \text{mPL}=10(10)-38=100-38 \\ \text{mPL}=62\degree \end{gathered}`