Question

Find the equation of the perpendicular to 5x+3y=7 and passing through (2,3)

Answer 1

The first step to solve this problem is arrange the equation in the standard line equation form, which is given below:

`y\text{ = m}\cdot x\text{ + }b`

y = m*x + b

Where "m" is the slope of the line and "b" is the constant shift. To find the perpendicular line we need to find a line with the slope as shown below:

`m_1\text{ =-}(1)/(m)\text{ }`

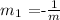
m1 = -1/m

We need to arrange the given expression.

`\begin{gathered} 5x\text{ + 3y = 7} \\ 3y\text{ = 7 - 5x} \\ y\text{ = -}(5)/(3)x\text{ + }(7)/(3) \end{gathered}`

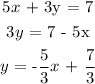
5x + 3y = 7

3y = 7 - 5x

y = (-5/3)x + 7/3

The slope of the given line is -5/3 to find the perpendicular line we need to find the slope -1/m. Which is done below:

m1 = -1/(-5/3) = -1*(-3/5) = 3/5

The perpendicular line we want has the a slope of 3/5. We can find the constant shift by applying the given point.

Perpendicular:

y = (3/5)*x + b

Applying the point:

3 = (3/5)*2 + b

3 = 6/5 + b

b = 3 - 6/5 = 15/5 - 6/5 = 9/5

Therefore the perpendicular line is given by:

y = (3/5)*x + 9/5