Question

In the diagram, es and PR bisect each other at point T. Find the measure of

Answer 1

Since QS and PR bisect each other at point T, triangles QTP and RTS are similar. Hence, we ca draw the following picture:

and we can see that x+48 must be equal to 2x:

`2x=x+48`

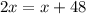
and we can solve this equation for the unknow x as

`\begin{gathered} 2x-x=48 \\ x=48 \end{gathered}`

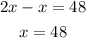
Now, with the value x, the angle P is equal to

`\begin{gathered} P=48+48 \\ P=96 \end{gathered}`

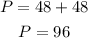
and the answer is a.