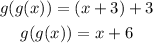We are given the following functions:
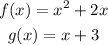
We are asked to determine the following composition:
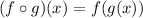
This means that where we have "x" in f we will replace it for the function g, like this:
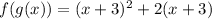
Simplifying we get:
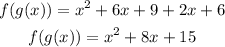
Now we are asked to determine the following composition:
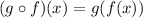
This means that where there is "x" in g we will replace it by f:
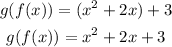
Now we are asked to determine:
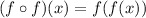
Replacing the value of f in f:
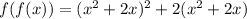
Simplifying:
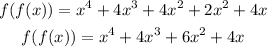
Finally, we are asked to determine the following composition:
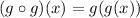
Replacing we get: