Given:
The total cost of the clothing, C=$765.47.
The shipping weight, W=29 lb. 12 oz.
The sales tax rate, R=9.0%.
The shipping weight in lb is,

Given, shipping charges are $5.94 for 15 lb. For every additional lb. or fraction of a lb. above 15 lbs., the shipping charge is $0.12 per lb.
The shipping weight above 15 lb is,
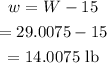
Now, the total shipping charge for 29.0075 lb is,
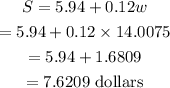
Now, the pre tax cost of the item is,
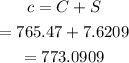
Now, the sales tax of the item is,

Now, the total cost of the order is,
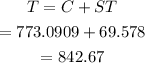
So, the total cost of the order can be $842.10.