Question

A ball is dropped from a tower. The table shows the heights of the ball's bounces, which form a geometric sequence. Describe in words how you would find the height of the next bounce?

Answer 1

to find the height of the next bounce, just replace the x value in the function

`f(x)=36x^2-228x+392`

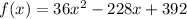
the heigth of next bounce is 56 ft}

Step-by-step explanation

Step 1

find the equation of the quadratic function, so

i) set the equations

a quadratic function is in the form

`f(x)=ax^2+bx+c`

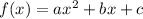
so, we can replace the known coordinates for find a, b and c

so

a)

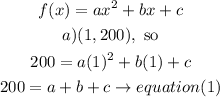
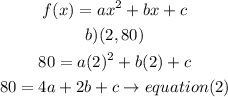
`\begin{gathered} f(x)=ax^2+bx+c \\ a)(1,200),\text{ so} \\ 200=a(1)^2+b(1)+c \\ 200=a+b+c\rightarrow equation(1) \end{gathered}`

b)

`\begin{gathered} f(x)=ax^2+bx+c \\ b)(2,80) \\ 80=a(2)^2+b(2)+c \\ 80=4a+2b+c\rightarrow equation(2) \end{gathered}`

c)

`\begin{gathered} f(x)=ax^2+bx+c \\ c)(3,32) \\ 32=a(3)^2+(3)x+c \\ 32=9a+3b+c\rightarrow equation\text{ (3)} \end{gathered}`

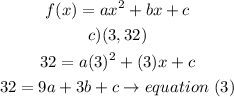
Step 2

solve the equations

`\begin{gathered} 200=a+b+c\rightarrow equation(1) \\ 80=4a+2b+c\rightarrow equation(2) \\ 32=9a+3b+c\rightarrow equation\text{ (3)} \end{gathered}`

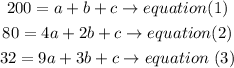
a) isolate x in equation (1) and (2) , then let c= c

so

`\begin{gathered} 200=a+b+c\rightarrow equation(1) \\ c=200-a-b \\ and \\ 80=4a+2b+c\rightarrow equation(2) \\ c=80-4a-2b \\ c=c\text{ , so} \\ 200-a-b=80-4a-2b \\ 200-80=-4a-2b+a+b \\ 120=-3a-b\rightarrow equation(4) \end{gathered}`

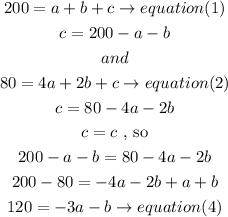
b)isolate x in equation (1) and (3) , then let c= c

`\begin{gathered} 32=9a+3b+c \\ c=32-9a-3b \\ C=C,\text{ so} \\ 200-a-b=32-9a-3b \\ 300-32=-9a-3b+a+b \\ 168=-8a-2b\rightarrow equation(5) \end{gathered}`

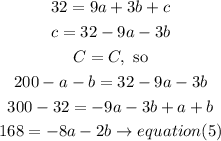
c) now, use equation (4) and equation(5) to find a and b

`\begin{gathered} 120=-3a-b\rightarrow equation(4) \\ 168=-8a-2b\rightarrow equation(5) \end{gathered}`

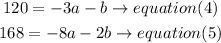
i)isolate b in both sides, then let b=b

`\begin{gathered} 120=-3a-b\rightarrow equation(4) \\ b=-3a-120 \\ \text{and} \\ 168=-8a-2b\rightarrow equation(5) \\ 168+8a=-2b \\ b=(168+8a)/(-2) \\ b=-84-4a \\ B=B,\text{ so} \\ -3a-120=-84-4a \\ -3a+4a=-84+120 \\ a=36 \end{gathered}`

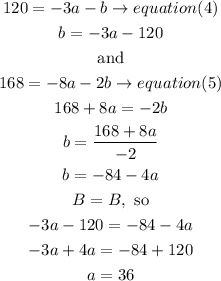
replace to find b

`\begin{gathered} b=-3a-120 \\ b=-3(36)-120 \\ b=-108-120=-228 \\ b=-228 \end{gathered}`

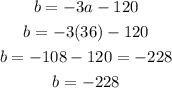
finally, replacei n equation (1) to find c

`\begin{gathered} 200=a+b+c\rightarrow equation(1) \\ 200=36-228+c \\ 200=192+c \\ 200+192=c \\ c=392 \end{gathered}`

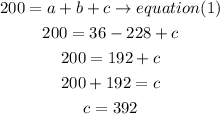
therefefore,

`f(x)=36x^2-228x+392`

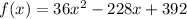
Step 3

now, we have the function

`f(x)=36x^2-228x+392`

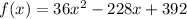
so

to find the height of the next bounce, just replace the x value in the function

`f(x)=36x^2-228x+392`

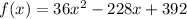
so, when bounce = 4,

let

x=4

`\begin{gathered} f(x)=36x^2-228x+392 \\ f(4)=36(4)^2-228(4)+392 \\ f(4)=56 \end{gathered}`

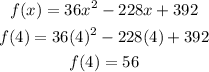
so, the heigth of next bounce is 56 ft

56 ft

I hope this helps you