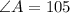Given ABC has interior angle measures with:

Question

asked Jun 7, 2023 214k views

1 Answer

Jaredpalmer · Answer 1 · 2023-06-12T05:36:20+0000

For this exercise it is important to remember the de sum of the interior angles of a triangle is 180 degrees.

For this case, you have the triangle ABC, and according to the information given in the exercise:

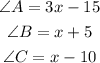
$\begin{gathered} \angle A=3x-15 \\ \angle B=x+5 \\ \angle C=x-10 \end{gathered}$

Knowing the above, you can set up the following equation:

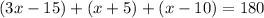
Now you must solve for "x":

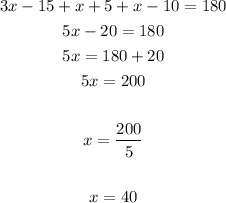
$\begin{gathered} 3x-15+x+5+x-10=180 \\ 5x-20=180 \\ 5x=180+20 \\ 5x=200 \\ \\ x=(200)/(5) \\ \\ x=40 \end{gathered}$

Now, substitute the value of "x" into this equation:

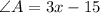
$\angle A=3x-15$

Evaluating, you get that the measure of the angle A is:

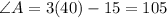
$\angle A=3(40)-15=105\degree$

The answer is:

$\angle A=105\degree$