Question

Abby, who has a mass of 45.0 kg, is riding at 40.0 m/s in her red sports car when she must suddenly slam on the brakes to avoid hitting a deer crossing the road. She strikes the airbag, that brings her body to a stop in 0.500 s. What average force does the seatbelt exert on her?What if Abby had not been wearing her seatbelt and not had an airbag, then the windshield would have stopped her head in 0.002 s. What average force would the windshield have exerted on her?I need to do the following:1. Solve for force in each scenario.2. Explain the significance of time on the overall force and link to Newtons first and second laws.3. Show all work.

Answer 1

Given,

The mass of Abby, m=45.0 kg

The speed of the car, u=40.0 m/s

The time interval in which Abby was stopped, t=0.500 s

The time interval in which Abby would have been stopped by the windshield, t₀=0.002 s

From the equation of motion,

`v=u+at`

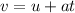
Where v is the final velocity. In this case, as Abby is stopped, the final velocity is 0 m/s. And a is the acceleration.

On substituting the known values,

`\begin{gathered} 0=40.0+a*0.500 \\ \Rightarrow a=(-40.0)/(0.500) \\ =-80m/s^2 \end{gathered}`

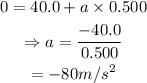
From Newton's first law, to bring an object in motion to the rest force needs to be applied.

The force that brings Abby to rest is given by Newton's second law which is,

`F=ma`

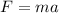
Thus the force that the seatbelt exerts on her is

`\begin{gathered} F=45.0*-80.0 \\ =-3600\text{ N} \end{gathered}`

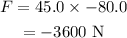
Thus the force exerted by the seatbelt is 3600 N

From the equation of motion, the acceleration of Abby when she is stopped by the windshield can be calculated as,

`v=u+a_0t_0`

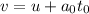
On substituting the known values,

`\begin{gathered} 0=40.0+a_0*0.002 \\ a_0=(-40.0)/(0.002) \\ =-20*10^3m/s^2 \end{gathered}`

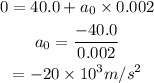
From Newton's second law, the force exerted by the windshield is,

`\begin{gathered} F_0=ma_0 \\ =45*20*10^3 \\ =900\text{ kN} \end{gathered}`

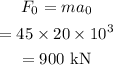
Thus the force that the windshield would exert on Abby is 900 kN.

As the acceleration is inversely proportional to time, as the time interval reduces the acceleration increases. And the increase in acceleration will increase the force applied.