Question

Find all values of j for which the quadratic equation has one real solution.6x^2-5x+j=0Write your answer as an equality or inequality in terms of j.

Answer 1

Given the question in the question tab, the following are the solution steps to solve the problem.

Step 1: Define the conditions for which a quadratic equation will have one real solution.

A quadratic equation has one real solution if the discriminant of the equation equals to zero. This means that:

`\begin{gathered} D=0 \\ D=b^2-4ac=0 \end{gathered}`

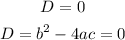
Step 2: Write out the quadratic equation given and the parameters

`\begin{gathered} 6x^2-5x+j=0 \\ By\text{ comparisonn with }ax^2+bx+c=0, \\ a=6,b=-5,c=j \end{gathered}`

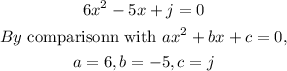
Step 3: Substitute the values in step 2 in the equation in step 1 to solve for j

`\begin{gathered} D=b^2-4ac=0 \\ (-5^2)-4(6)(j)=0 \\ 25-24j=0 \\ 25=24j \\ j=(25)/(24) \end{gathered}`

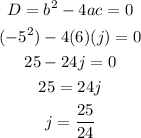
Hence, the given quadratic equation will have one real solution when the value of j is equal to 25/24