Question

Let cos(2x) - cos(x) = 0, where 0° sx s 180°. What are the possible values for x?O 60° onlyO 120° onlyO 0° or 120°O 60° or 180°

Answer 1

Given the equation:

`\cos \mleft(2x\mright)-cos\mleft(x\mright)=0`

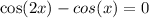
First, we will express the cos (2x) in terms of cos (x) using the angle double rule:

`\cos (2x)=2\cos ^2(x)-1`

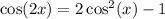
So, the given equation will be:

`\begin{gathered} 2\cos ^2(x)-1-\cos (x)=0 \\ 2\cos ^2(x)-\cos (x)-1=0 \end{gathered}`

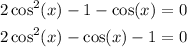
The last equation has the form of the quadratic equation, so we will factor the equation:

`\begin{gathered} (2\cos +1)(\cos x-1)=0 \\ 2\cos x+1=0\rightarrow\cos x=-(1)/(2)\rightarrow x=\cos ^(-1)(-(1)/(2))=120\degree \\ \cos x-1=0\rightarrow\cos x=1\rightarrow x=\cos ^(-1)(1)=0\degree \end{gathered}`

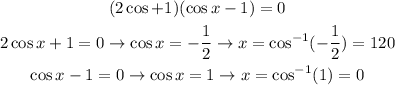
So, the answer will be option 3) x = 0° or 120°