Answer:
![x=\frac{17+\sqrt[]{241}}{8},\frac{17-\sqrt[]{241}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/efqbvcc8rwfl8ajaq88iqp476h20uvzmhg.png)
Step-by-step explanation:
Given the below function;
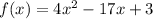
Note that a quadratic equation in standard form is generally given as;
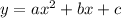
If we compare both of the equations above, we can deduce that;
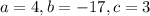
We'll now use the below quadratic formula to solve for the values of x as seen below;
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{17\pm\sqrt[]{(-17)^2-4\cdot4\cdot3}}{2\cdot4} \\ x=\frac{17\pm\sqrt[]{289-48}}{8} \\ x=\frac{17\pm\sqrt[]{241}}{8} \\ \therefore x=\frac{17+\sqrt[]{241}}{8},\frac{17-\sqrt[]{241}}{8} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ejzjzbjs0g96sift5nnnirhomgvkiccan3.png)