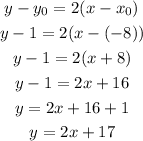Let's start with the standard form of a line:

"m" is the slope of this line.
The slopes of two perpendicular lines, m1 and m2, have the relation:
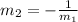
So, if we want the slope of a line perpendicular to a known line, we can simply use its slope to it.
The given line here is:
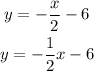
So, the slope of this line is:
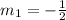
To find the slope of a lie perpendicular to it, we use the above relation:
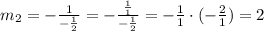
So, the slope of our line is 2.
In the slope-intercept form, this is:
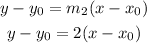
Now, we just need to have x0 and y0, which are the coordinates of a point in the line. We are given the point (-8,1), which means that:
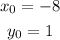
So: